Game theory is useful when an "opponent" responds to a particular behavior: i.e. a strategy may be met by a strategy during a contest:

Under these circumstances, payoffs must be calculated for all combinations of strategies by contestants.

This is usually calculated for two contestants (i.e., a "two player game").

Some "games" that you've already seen:

Hawk/Dove contests

Tit for tat reciprocity models

The Prisoner's dilemma

 

In this class you will learn to solve specific types of simple games. 

When the roles of the two opponents can be exchanged without changing the outcomes, the game is said to be symmetrical.

 

When the roles cannot be exchanged the game is asymmetrical

i) when two opponents do not have equal access to the same strategies

ii) when two opponents have different probabilities of "winning" a contest

iii) when two opponents receive different payoffs for "winning"

 

To solve these games, we must seek the Evolutionary Stable Strategy (or ESS)

In a symmetric game the ESS is the strategy that is the best either opponent can do given the options (thus it cannot be "invaded" by an alternative.... it is stable)

In an asymmetric game, the ESS will be a combination of a strategy by player 1 and another by player 2 that cannot be invaded by other combinations.

 

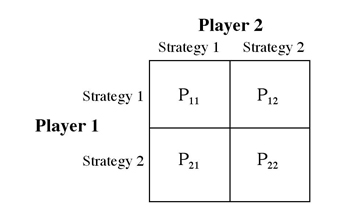
The simplest symmetric game involves two players that can adopt either of two strategies (i.e., four possible combinations):

First thing to remember: In a symmetric 2 x 2 table, there is always an ESS

There are four possible ways this ESS may be achieved depending on the relative payoffs of playing one strategy vs. the other given an opponent's possible plays. These are described as the four cases below.

To figure out which of the four cases is present, you must consider the possible scenarios of relative (higher or lower) payoffs accruing to player 1, given what Player 2 does..... Use dots dots to represent which strategy by player 1 gives the higher payoff when Player 2 plays strategy 1 vs. when they play strategy 2.

Here's how to do that: Begin by looking "down" the Strategy 1 column for Player 2 and asking, of the two possible payoffs to Player 1, which gives the higher value? This is the strategy they should choose and it can be denoted by putting a large dot into the square with the higher payoff.

Now, repeat this procedure, but this time look "down" the Strategy 2 column for Player 2... given the payoffs, what should Player one do? For the two squares in questions, put a dot in the square with the highest value.

You will now have two dots on the matrix in one of the four possible outcomes below:

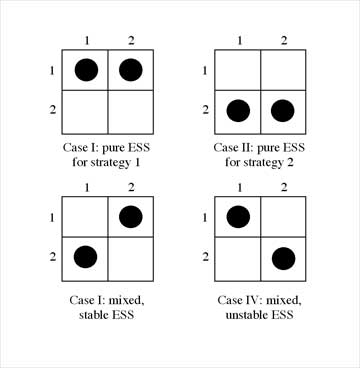
In Case I, Player 1does better by playing strategy 1, no matter what strategy Player 2 plays.

Thus, strategy 1 is a Pure ESS whenever a) P₁₁ > P₂₁ and b) P₁₂ > P₂₂

In Case II, Player 1 does better by playing strategy 2, no matter what Player 2 does.

Now Strategy 2 is the Pure ESS (i.e. P₁₁ < P₂₁ and P₁₂ < P₂₂).

In Case III, Player 1 should always play the opposite strategy to that played by Player 2. Such a system will stabilize at an equilibrium in which each player does best by playing Strategy 1 some fraction (f) of the time and Strategy 2 (1 - f) of the time. This is called a Mixed Stable ESS.

 

In this scenario, there are two ways this ESS may be achieved:

Each animal plays Strategy 1 (f) of the time and Strategy 2 (1 - f) of the time.... a "behavioral polymorphism".

Of the total population, a proportion (f) of the animals play Strategy 1 and (1 - f) of the animals play Strategy 2.... a "genetic polymorphism".

 

Case III occurs when P₁₁ < P₂₁ and P₁₂ > P₂₂ and the equilibrium frequency of playing strategy 1 (f₀) can be calculated as: f₀ = (P₁₂– P₂₂)/((P₁₂– P₂₂) + (P₂₁– P₁₁))

 

How is this result obtained?

This result is obtained by considering the payoff an individual playing only strategy 1 gets from encountering (f₁) opponents playing Strategy 1 and (1 - f₁) opponents playing strategy 2 for the full range of f₁ (i.e, from 0.0... no one playing strategy 1.... to 1.0... everyone playing strategy 1). This is a conditional payoff:

The average payoff for playing Strategy 1 can be estimated as:

(i) PO₁ = f₁P₁₁ + (1 - f₁)P₁₂ = P₁₂ + (P₁₁ - P₁₂)f₁

 

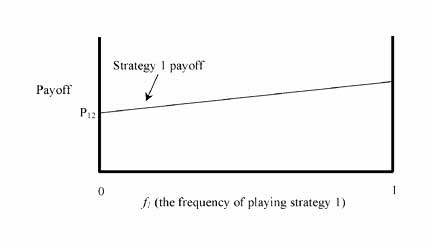
you may note that this equation is the expression for a line of slope (P₁₁ - P₁₂) and Y intercept of P₁₂

Similarly, the average payoff of playing Strategy 2 is:

(ii) PO₂ = f₁P₂₁ + (1 - f₁)P₂₂ = P₂₂ + (P₂₁ - P₂₂)f₁

another line, this one with slope of (P₂₁ - P₂₂) and intercept of P₂₂

a) By definition for Case III; P₁₂ > P₂₂

Thus, we know that this second line intercepts the Y axis below the first line.

b) Also for Case III: P₂₁ > P₁₁

Adding and rearranging these two inequalities, we see that P₂₁ - P₂₂ > P₁₁- P₁₂

These are the slopes of the two lines, with the slope for playing strategy 2 is greater:

 

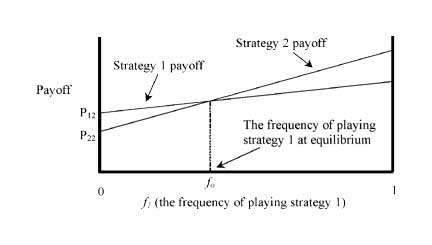
An equilibrium exists where the payoff of playing strategy 1 equals the payoff of strategy 2 (where the lines intercept). This can be found by setting the payoff equations (i) and (ii) equal to one another. This yields the equation given above for a stable equilibrium.

In Case IV, Player 1 should always play the same strategy to that played by Player 2. This is the outcome whenever a) P₁₁ > P₂₁ and P₁₂ < P₂₂. Following similar computations as above, you will find that the relative position of Y intercepts and magnitude of the slopes are reversed. Again the lines cross, so there is an equilibrium frequency of playing strategy 1 (f₀) where the two payoffs are equivalent. Now, however, the equilibrium is unstable and if the population is not precisely at (f₀), there will be a shift away from the equilibrium towards either pure Strategy 1 or pure Strategy 2.

In general, the strategy with the higher frequency at (f₀) is the most likely one to be found. Why is this?

Plotting the payoff lines for Case IV (as was done for Case III) may help you understand these results.

Click here for a couple of practice questions using game theory

Some questions to consider:

What do you expect to be differences in the success of strategy 1 vs strategy 2 when strategy 1 begins as: a) a rare strategy; b) a very common strategy, and when both strategies are present in equal frequencies?

In the Hawk/Dove game, there are costs for fighting and rewards for winning outright access to a resource. Under what mathematical circumstances will a "pure" Hawk be an ESS?